Cad é an fad easghluaiseach X agus an fad easghluaiseach Y?
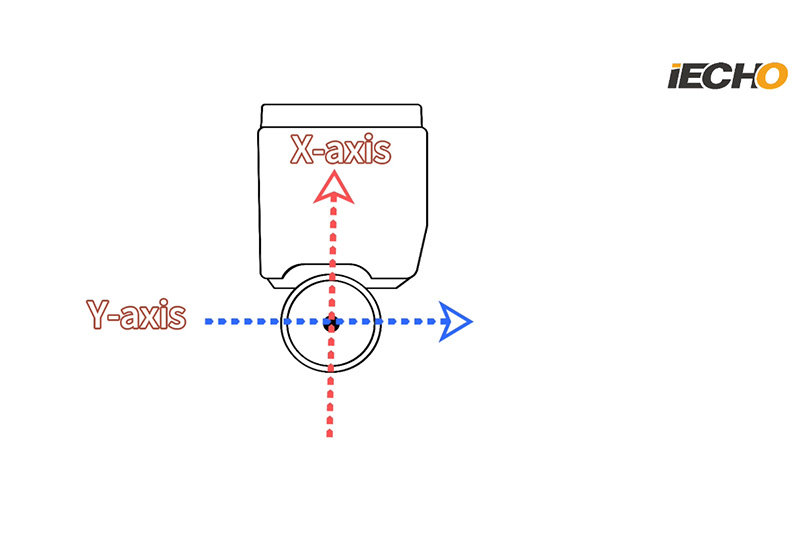
Is é atá i gceist againn le neamhrialtacht an diall idir lár bharr na lanna agus an uirlis ghearrtha.
Nuair a chuirtear an uirlis ghearrtha sa Caithfidh barr an lann, i gcás an chinn ghearrtha, a bheith suite ar chomhchéim le lár an uirlis ghearrtha. Má tá diall ann, is é seo an fad easghluaiseach.
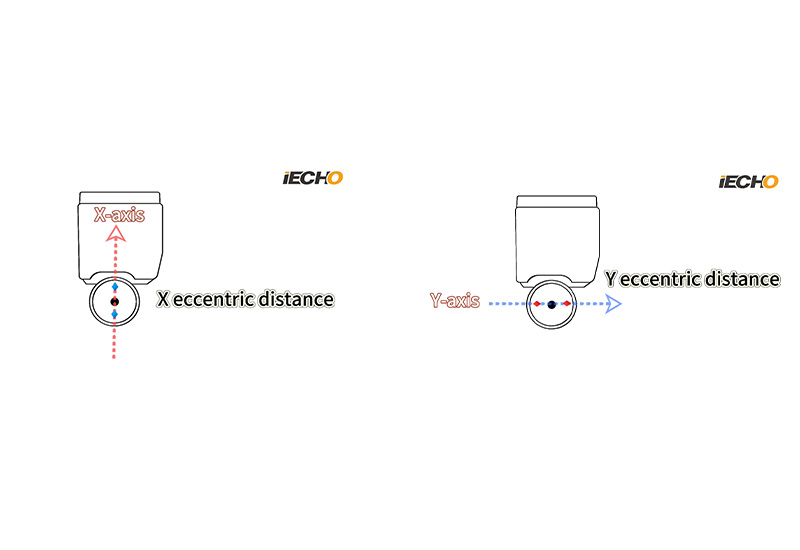
Is féidir achar easghluaiseachta uirlise a roinnt ina achar easghluaiseachta X agus Y. Nuair a fhéachaimid ar an radharc barr den cheann gearrtha, tagraimid don treo idir an lann agus cúl na lann mar an ais-X agus tugtar an ais-y ar threo an ais-X ingearach atá dírithe ar bharr na lann.
Nuair a tharlaíonn diall bharr na lanna ar an ais-X, tugtar achar easghluaiseach X air. Nuair a tharlaíonn diall bharr na lanna ar an ais-Y, tugtar achar easghluaiseach Y air.
Nuair a tharlaíonn achar easghluaiseachta Y, beidh méideanna gearrtha éagsúla i dtreonna gearrtha éagsúla.
D’fhéadfadh fadhb a bheith ag roinnt samplaí fiú maidir le líne gearrtha i gcás nach ngearrtar an nasc. Nuair a bhíonn achar easghnéach X ann, athróidh an cosán gearrtha iarbhír.
Conas a choigeartú?
Agus ábhair á ngearradh agat, an mbíonn cásanna ann ina mbíonn méideanna gearrtha difriúla i dtreonna gearrtha difriúla, nó go mbíonn fadhb leis an líne gearrtha i roinnt samplaí fiú nuair nach ngearrtar an nasc? Fiú tar éis gearradh CCD, d'fhéadfadh imill bhána a bheith ar roinnt píosaí gearrtha. Tá an cás seo mar gheall ar an gceist maidir le fad easghluaiseachta Y. Conas a bhíonn a fhios againn an bhfuil an fad easghluaiseachta Y ann? Conas é a thomhas?
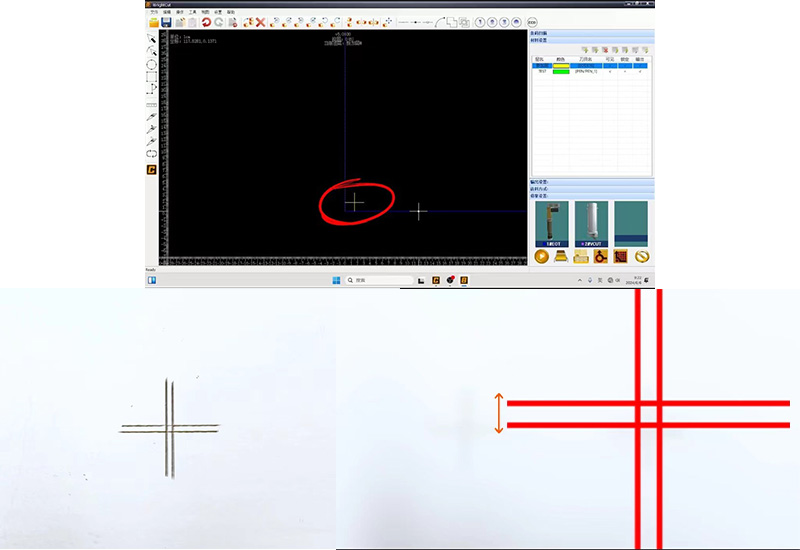
Ar dtús, ba chóir dúinn IBrightCut a oscailt agus an grafaic tástála CCD a aimsiú, agus ansin an patrún seo a shocrú mar an uirlis ghearrtha atá uait le haghaidh tástála gearrtha. Is féidir linn páipéar neamhghearrtha a úsáid le haghaidh tástála ábhair. Ansin is féidir linn sonraí a sheoladh le gearradh. Feicimid gur líne ghearrtha tras-chruthach í na sonraí tástála, agus gach cuid den líne á gearradh faoi dhó ó threoracha difriúla. Is é an bealach a ndéanaimid an fad easghluaiseachta Y a mheas ná a sheiceáil an bhfuil líne an dá ghearradh ag forluí. Má dhéanann siad, léiríonn sé nach bhfuil an ais-Y easghluaiseachta. Agus mura bhfuil, ciallaíonn sé go bhfuil easghluaiseacht san ais-Y. Agus is leath an achair idir an dá líne ghearrtha an luach easghluaiseachta seo.
Oscail an CutterServer agus líon isteach an luach tomhaiste sa pharaiméadar achair easghéartach Y agus ansin déan tástáil. Oscail an CutterServer agus líon isteach an luach tomhaiste sa pharaiméadar achair easghéartach Y agus ansin déan tástáil. Ar dtús, breathnaigh ar éifeacht ghearradh an phatrúin tástála i ndoimhneacht cheann an ghearrtha. Is féidir leat a fheiceáil go bhfuil dhá líne ann, ceann inár lámh chlé agus an ceann eile inár lámh dheas. Tugtar líne A ar an líne a ghearrann ón tosaigh go dtí an cúl, agus os a choinne sin, tugtar líne B uirthi. Nuair a bhíonn líne A ar an taobh clé, bíonn an luach diúltach, agus a mhalairt. Agus an luach easghéartach á líonadh isteach, ba chóir a thabhairt faoi deara nach mbíonn an luach seo an-mhór de ghnáth, ní gá dúinn ach é a mhionchoigeartú.
Ansin, gearr an tástáil arís agus is féidir go mbeidh forluí foirfe idir an dá líne, rud a léiríonn go bhfuil an t-easghné bainte. Ag an am seo, is féidir linn a fháil amach nach mbeidh cásanna ann ina mbeidh méideanna gearrtha difriúla i dtreonna gearrtha difriúla agus nach mbeidh an nasc gearrtha.
An coigeartú achair easghluaiseach X:
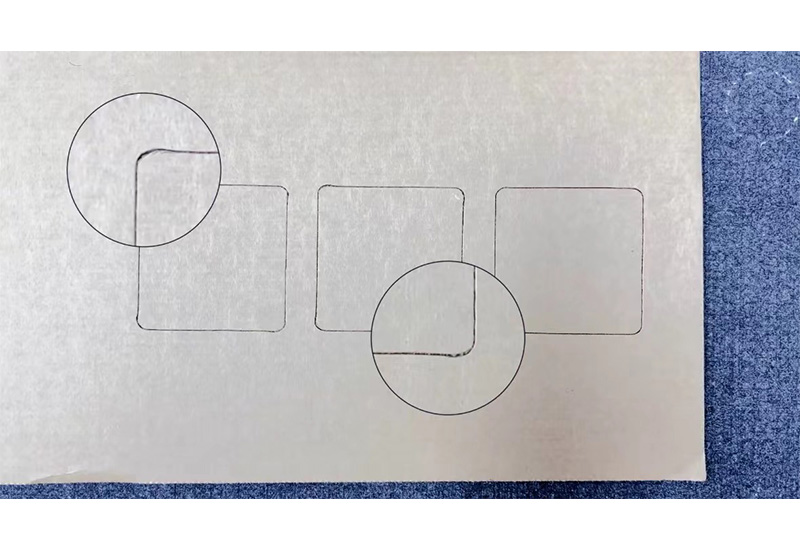
Nuair a bhíonn an ais-X easghluaiseach, athróidh suíomh na línte gearrtha iarbhír. Mar shampla, nuair a rinneamar iarracht patrún ciorclach a ghearradh, fuair muid grafaic eachtrannach. Nó nuair a dhéanaimid iarracht cearnóg a ghearradh, ní féidir na ceithre líne a dhúnadh go hiomlán. Conas a bhíonn a fhios againn an bhfuil an t-achar easghluaiseach X? Cé mhéad coigeartaithe atá ag teastáil?
Ar dtús, déanaimid sonraí tástála in IBrightCut, tarraingímid dhá líne den mhéid chéanna, agus tarraingímid líne treorach sheachtrach ar an taobh céanna den dá líne leis an líne tagartha, agus ansin seolaimid an tástáil gearrtha. Má sháraíonn ceann den dá líne gearrtha an líne tagartha nó mura sroicheann sí í, léiríonn sé go bhfuil an ais X easghluaiseach. Tá dearfach agus diúltach ag luach an achair easghluaiseach X freisin, atá bunaithe ar líne tagartha threo Y. Má sháraítear líne A, tá easghluaiseacht an ais X dearfach; má sháraíonn líne B, tá easghluaiseacht an ais X diúltach. Is é an paraiméadar a chaithfear a choigeartú ná an t-achar a sháraíonn nó nach sroicheann an líne tagartha atá ag an líne tomhaiste.
Oscail an Cutterserver, aimsigh deilbhín an uirlis tástála reatha, cliceáil ar dheis agus aimsigh an fad easghluaiseachta X sa cholún socruithe paraiméadair. Tar éis an choigeartú, déan an tástáil gearrtha arís. Nuair is féidir na pointí tuirlingthe ar an taobh céanna den dá líne a nascadh go foirfe leis an líne tagartha, léiríonn sé sin gur coigeartaíodh an fad easghluaiseachta X. Ba chóir a thabhairt faoi deara go gcreideann go leor daoine gur ró-ghearradh is cúis leis an gcás seo, rud atá mícheart. Déanta na fírinne, is é an fad easghluaiseachta X is cúis leis. Ar deireadh, is féidir linn tástáil a dhéanamh arís agus an patrún iarbhír tar éis gearrtha comhsheasmhach leis na sonraí gearrtha ionchuir, agus ní bheidh aon earráidí sna grafaicí gearrtha.
Am an phoist: 28 Meitheamh 2024